Triple Integrals in Cylindrical Coordinates

When the function to be integrated has a cylindrical symmetry, it is sensible to change the variables into cylindrical coordinates and then perform integration.

In R³ the integration on domains with a circular base can be made by the passage in cylindrical coordinates; the transformation of the function is made by the following relation: 

$f(x,y,z) \rightarrow f(\rho \cos \varphi, \rho \sin \varphi, z)$

The domain transformation can be graphically attained, because only the shape of the base varies, while the height follows the shape of the starting region. Also in switching to cylindrical coordinates, the $dx\, dy\, dz$ differentials in the integral become $\rho \, d\rho \,d\varphi \,dz$.

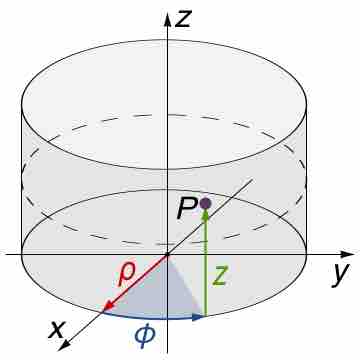
Cylindrical Coordinates

Cylindrical coordinates are often used for integrations on domains with a circular base.

Example 1

The region is:

 $D = \{ x^2 + y^2 \le 9, \ x^2 + y^2 \ge 4, \ 0 \le z \le 5 \}$

If the transformation is applied, this region is obtained: 

$T = \{ 2 \le \rho \le 3, \ 0 \le \varphi \le 2\pi, \ 0 \le z \le 5 \}$

because the z component is unvaried during the transformation, the $dx\, dy\, dz$ differentials vary as in the passage in polar coordinates: therefore, they become: $\rho \, d\rho \,d\varphi \,dz$. Finally, it is possible to apply the final formula to cylindrical coordinates: 

$\displaystyle{\iiint Df(x,y,z)dx\,dy\,dz=\iiint Tf(\rho\cos\varphi,\rho\sin\varphi,z)\rho\, d\rho \,d\varphi \,dz}$

This method is convenient in case of cylindrical or conical domains or in regions where it is easy to individuate the $z$ interval and even transform the circular base and the function.

Example 2

The function $f(x,y,z) = x^2 + y^2 + z$ is and as integration domain this cylinder: 

$D = \{ x^2 + y^2 \le 9, \ -5 \le z \le 5 \}$

The transformation of $D$ in cylindrical coordinates is the following: 

$T = \{ 0 \le \rho \le 3, \ 0 \le \phi \le 2 \pi, \ -5 \le z \le 5 \}$

while the function becomes:

 $f(\rho \cos \varphi, \rho \sin \varphi, z) = \rho^2 + z$

Therefore, the integral becomes:

$\begin{aligned}\displaystyle{\iiint_D (x^2 + y^2 +z) \, dx\, dy\, dz} &\displaystyle{= \iiint_T ( \rho^2 + z) \rho \, d\rho\, d\phi\, dz} \\ &= \int_{-5}^5 dz \int_0^{2 \pi} d\phi \int_0^3 ( \rho^3 + \rho z )\, d\rho\\ &= 2 \pi \int_{-5}^5 \left[ \frac{\rho^4}{4} + \frac{\rho^2 z}{2} \right]_0^3 \, dz\\ &= 2 \pi \int_{-5}^5 \left( \frac{81}{4} + \frac{9}{2} z\right)\, dz\\ &= 405 \pi \end{aligned}$