Expected Values of Discrete Random Variables

Discrete Random Variable

A discrete random variable $X$ has a countable number of possible values. The probability distribution of a discrete random variable $X$ lists the values and their probabilities, such that $x_i$ has a probability of $p_i$. The probabilities $p_i$ must satisfy two requirements:

1. Every probability $p_i$ is a number between 0 and 1.
2. The sum of the probabilities is 1: $p_1+p_2+\dots + p_i = 1$.

Expected Value Definition

In probability theory, the expected value (or expectation, mathematical expectation, EV, mean, or first moment) of a random variable is the weighted average of all possible values that this random variable can take on. The weights used in computing this average are probabilities in the case of a discrete random variable.

The expected value may be intuitively understood by the law of large numbers: the expected value, when it exists, is almost surely the limit of the sample mean as sample size grows to infinity. More informally, it can be interpreted as the long-run average of the results of many independent repetitions of an experiment (e.g. a dice roll). The value may not be expected in the ordinary sense—the "expected value" itself may be unlikely or even impossible (such as having 2.5 children), as is also the case with the sample mean.

How To Calculate Expected Value

Suppose random variable $X$ can take value $x_1$ with probability $p_1$, value $x_2$ with probability $p_2$, and so on, up to value $x_i$ with probability $p_i$. Then the expectation value of a random variable $X$ is defined as: $E[X] = x_1p_1 + x_2p_2 + \dots + x_ip_i$, which can also be written as: $E[X] = \sum x_ip_i$.

If all outcomes $x_i$ are equally likely (that is, $p_1 = p_2 = \dots = p_i$), then the weighted average turns into the simple average. This is intuitive: the expected value of a random variable is the average of all values it can take; thus the expected value is what one expects to happen on average. If the outcomes $x_i$ are not equally probable, then the simple average must be replaced with the weighted average, which takes into account the fact that some outcomes are more likely than the others. The intuition, however, remains the same: the expected value of $X$ is what one expects to happen on average.

For example, let $X$ represent the outcome of a roll of a six-sided die. The possible values for $X$ are 1, 2, 3, 4, 5, and 6, all equally likely (each having the probability of $\frac{1}{6}$). The expectation of $X$ is: $E[X] = \frac{1x_1}{6} + \frac{2x_2}{6} + \frac{3x_3}{6} + \frac{4x_4}{6} + \frac{5x_5}{6} + \frac{6x_6}{6} = 3.5$. In this case, since all outcomes are equally likely, we could have simply averaged the numbers together: $\frac{1+2+3+4+5+6}{6} = 3.5$.

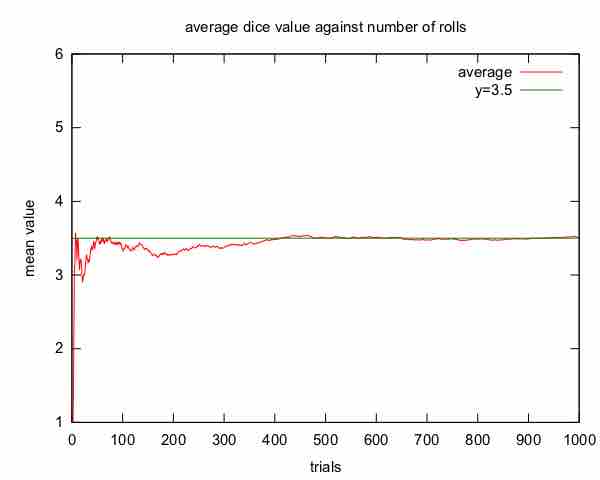
Average Dice Value Against Number of Rolls

An illustration of the convergence of sequence averages of rolls of a die to the expected value of 3.5 as the number of rolls (trials) grows.